Bending Behaviour of One Way Slab and Two Way Slab

One Way Slab and Two Way Slab

There are different slabs, but one-way slabs and two-way slabs are the most common slabs used in RCC construction. Today in this article, we know about the bending behaviour of the One Way slab and Two Way Slab.

As we know, if the ly/lx ratio is equal or greater than two, it is considered a one-way slab, and if the ly/lx ratio is less than two, then it is termed as a two-way slab.(lx = shorter span, ly = Longer span).

When both slabs are subjected to uniformly distributed load, the one-way slab bends in a shorter direction while the two-way slab bends in both directions.

Since one-way slab bends in one direction, that is a shorter direction; that’s why we provide main reinforcement along the shorter direction and distribution steel is provided along the longer span in one way slab.

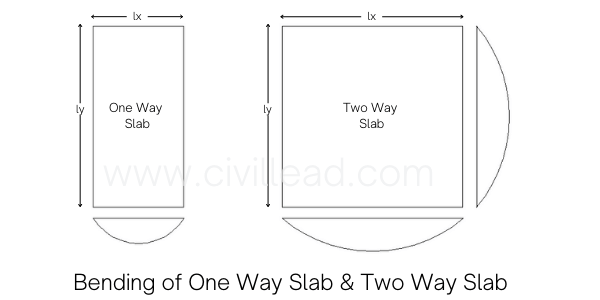
But Two-way slab bends in both directions; therefore, we provide main reinforcement in both directions: shorter and longer spans.

Also, Read – Difference Between One Way Slab and Two Way Slab.

Why does a One-way slab bend in one direction?

To understand the bending behaviour of a one-way slab, let’s take an example of a slab.

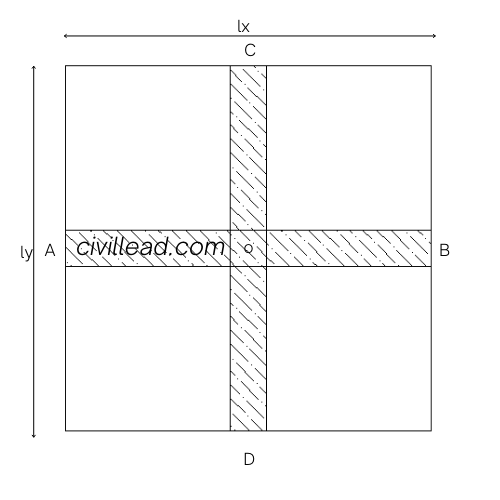
Now let’s assume the total uniformly distributed load on this slab is = W

Now let’s consider the two middle strips of unit width AC and BD along lx and ly directions respectively.

Wx = load carried by strip AC along the x-direction

Wy = load carried by strip BD along the y-direction

Total Load W = W_x + W_y

Due to the load W on strips, there will be deflection at the centre point. Now we have to calculate displacement at the centre point.

As we know, the deflection for simply supported beam subjected with uniformly distributed load is

δ = 5/385 Wl⁴/EI

Where

W = Uniformly distributed load

L = Length

E = Modulus of Elasticity

I = Moment of Inertia

Deflection along x direction = 5/385 W_xl_x⁴/EI

Deflection along x direction = 5/385 W_yl_y⁴/EI

Now equate these both equations.

5/385 W_xl_x⁴/EI = 5/385 W_yl_y⁴/EI

W_xl_x⁴/EI = W_yl_y⁴/EI

W_x = W_y(l_y/l_x)⁴

Now substitute the value of W_x

W = W_x +W_y

W_x = W – W_y

So

W – W_y = W_y(l_y/l_x)⁴

W = W_y + Wy(l_y/l_x)⁴

W = W_y[1 + (l_y/l_x)⁴]

W_y = W/[1 + (l_y/l_x)⁴]

Now Substitute the value of W_y to get the value of Wx

Wx = W(l_y/l_x)⁴/[1 + (l_y/l_x)⁴]

Now, If ly/lx = 2, then

Wy = W/{1 + (2)⁴ } = 0.05W

Wx = {W × (2)}⁴/1 + (2)4 = 0.95W

As we know, if the ratio of ly/lx is equal and greater than two, then it will be a one-way slab. Here, the load carried in y erection (longer span) is much lesser than the load carried by x-direction (shorter span). Therefore we provide main steel along a shorter span and distribution steel in a longer span.

Now If ly/lx = 1 then

Wy = W/1 + (1)⁴ = 0.5W

Wx = {W × (1)⁴}/1 + (1)4 = 0.5W

Here you can see the load carried in both directions is equal, and it is a two-way slab. Therefore in a two-way slab, we provide main steel in both directions.

I hope now you understand why one one-way slab bend only in one direction and two-way slab in both directions.

Thanks!

Also, Read

How to Calculate Quantity of Steel In One Way Slab? One Way Slab BBS

Bar Bending Schedule (BBS) – Importance, Advantages, Preparation

What is Lap Length? How to Calculate it? – Complete Guide

How to Calculate the Cutting Length of Stirrups for Beam and Column?

25+ Types of Beams Used In Construction