Table of Contents
Two Way Slab
A slab supported on four adjacent beams with a ratio of longer span to shorter span less than two that carry the load by flexure in both perpendicular directions refers to a two way slab.
If the L/B ( Length/width) ratio is less than two, a two way slab is provided. Uniformly loaded two way slabs deform into a dish or saucer-like shape, so bending moments develop in both directions.
In two-way slabs, main bars are placed in the shorter as well as longer span with the crank to prevent bending.
To learn how to calculate the steel quantity for the two way slab, let’s understand this with an example.
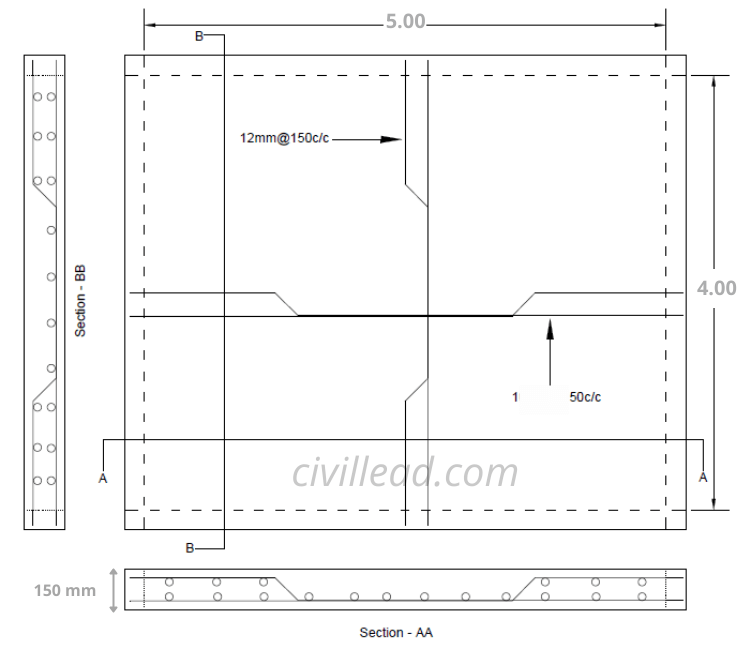
Given Data
We have a Two way slab drawing with the following data
Length = 5 Meter
Width = 4 Meter
Main Bar = 12 mm, Spacing – 150 mm c/c, Alternate bent up
Distribution Bar = 10 mm, Spacing – 150 mm c/c, Alternate bent up
Slab Thickness = 150 mm
Clear Cover = 20 mm
Development Length (Ld) = 40d
Step #1 – Bar Numbers
Nos of Bars = Total length/ spacing + 1
Nos of Main bar = 5000/150 +1
= 34 numbers
Nos of Distribution bar = 4000/150 +1
= 27 Numbers
Step# 2 – Cutting Length
For Main Bar
Cutting Length = Length (L) + 2 x Ld + (1 x 0.42D) – 2 x 1d
Where
L = Slab Clear Span
Ld = Development Length
0.42D = Inclined or crank length of the bar
1d = For 45° bend
Inclined Length D
D = Thickness of Slab – Top and Bottom cove – Bar Diameter
D = 150 – 2 x 20 – 12
D = 98 mm
Main Bar C L = 4000 + (2 x 40 x 12) + (0.42 x 98) – 2 x 12
= 4977.16 mm say 4977 mm or 4.977 meter
For Distribution Bar
Cutting Length = Length (L) + 2 x Ld + (1 x 0.42D) – 2 x 1d
Inclined Length D
D = Thickness of Slab – Top and Bottom cove – Bar Diameter
D = 150 – 2 x 20 – 10
D = 100 mm
Distribution Bar C L = 5000 + (2 x 40 x 10) + (0.42 x 100) – 2 x 10
= 5822.16 mm say 5822 mm or 5.822 meter

Step# 3 – Top Distribution Bar
For Shorter Span
Number of extra top bars = {(L/5) / spacing + 1} × 2(for both side)
= {(5000/5) / 150 +1} = 14 numbers
Length of the top bar = Clear Span of Slab + 2Ld
= 4000+(2 × 40 × 12)
= 4000 + 960
= 4960 mm or 4.96 m
For Longer Span
Number of Top bars = {(L/5) / spacing + 1} × 2(for both side)
= {(4000/5) / 150 + 1} × 2 = 12 Numbers
Length of the top bar = Clear Span of Slab + 2Ld
= 5000+(2 × 40 × 10)
= 5000 + 800
= 5800 mm or 5.8 m
Step# 4 – The calculation for Extra Top Bar
Extra top Bars are given at the top of the critical length (L/4/L/5) area to counter the bending moment.
For Shorter Span
Numbers of Extra Top Bars = {(L – 2L/5)/spacing of bar} × 2 Side
= {5000 – 2(5000/5)}/300 × 2
= 20 Numbers
Length of Top Extra Bar = L/5 + Ld = 4000/5 + 40 × 12 = 848 mm or 0.848 meter
For Longer Span
Numbers of Extra Top Bars = {(L – 2(L/5)/spacing of bar} × 2 Side
= {4000 – 2(4000/5)}/300 × 2
= 16 Numbers
Length of Top Extra Bar = L/5 + Ld = 5000/5 + 40 × 10 = 1040 mm or 1.04 meter
Step# 5 – Weight of Steel
Main Bar Weight = Nos of bar x Cutting Length x Bar Unit Weight (12 mm = 0.888)
= 34 x 4.977 x 0.888
= 150.26 kg
Distribution Bar Weight = Nos of bar x Cutting Length x Bar Unit Weight (10 mm = 0.0.617)
= 27 x 5.822 x 0.617
= 96.98 kg
Weight of Top Distribution bars
For Shorter span = Nos of bar x Cutting Length x Bar Unit Weight (12 mm = 0.888)
= 14 × 4.96 × 0.617
= 42.84 Kg
For longer span = Nos of bar x Cutting Length x Bar Unit Weight (10 mm = 0.617)
= 12 × 5.8 × 0.617
= 42.94 Kg
Weight of Top extra bars
For Shorter span = Nos of bar x Cutting Length x Bar Unit Weight (12 mm = 0.888)
= 20 × 0.848 × 0.888
= 15.06 Kg
For longer span = Nos of bar x Cutting Length x Bar Unit Weight (12 mm = 0.888)
= 16 × 1.04 × 0.617
= 10.26 Kg
Two Way Slab BBS
The bar bending schedule of two way slab is as follows.
| S.No. | Bar Description | Bar Shape | Nos | Length of Bar (m) | Total Length of Bar (M) | Bar Dia (mm) | Unit Weight (kg) | Total Weight (Kg) |
|---|---|---|---|---|---|---|---|---|
| 1 | Main Bar | 34 | 4.977 | 169.218 | 12 | 0.888 | 150.26 | |
| 2 | Distribution Bar | 27 | 5.822 | 157.194 | 10 | 0.617 | 96.98 | |
| 3 | Top Distribution Bar | |||||||
| Shorter Span | 14 | 4.96 | 69.44 | 10 | 0.617 | 42.84 | ||
| Longer Span | 12 | 5.8 | 69.6 | 10 | 0.617 | 42.94 | ||
| 4. | Extra Top Bar | |||||||
| Shorter Span | 20 | 0.848 | 16.96 | 12 | 0.888 | 15.06 | ||
| Longer Span | 16 | 1.04 | 16.64 | 10 | 0.617 | 10.26 |
I hope now you know how to calculate steel quantity for a two way slab. If you find the information valuable, please share it.
Thanks!
Also, Read
How To Calculate Steel Quantity For One Way Slab?
How to calculate the Cutting length of Stirrups for Beam and Columns?
How To Calculate Cement, Sand and Aggregate In Concrete?
How to calculate Brick Cement and Sand for Brickwork?
How to do Rate analysis for Concrete?